Interview Question on Greeks (Option Pricing) - 50 Q&A
1. What are Greek options in the context of financial derivatives?
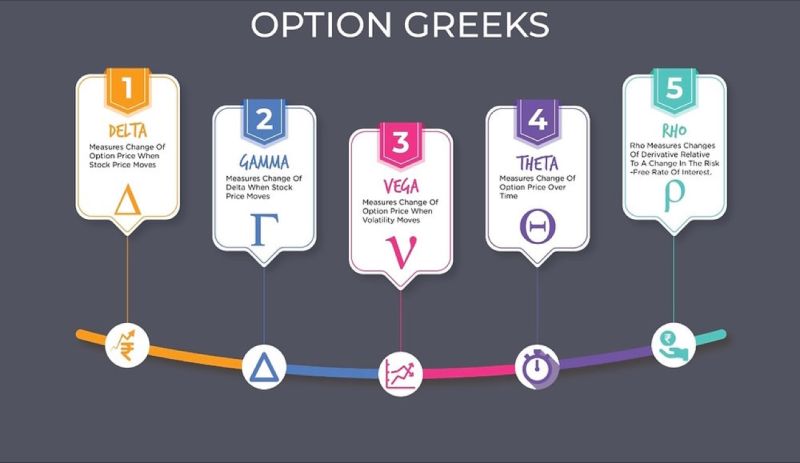
The variables that are used to assess risk in the options market are commonly referred to as “the Greeks.” A Greek symbol is used to designate each of these risks. The most common Greeks used include Delta (Δ), Gamma (Γ), Theta (Θ), Vega (ν), and Rho (Ρ) which are the first partial derivatives of the options pricing model.
These Greek letters represent key risk indicators and help traders, investors, and risk managers understand how changes in different variables can impact the value, price, and risk associated with options. The number or value associated with a Greek change over time. Therefore, sophisticated options traders may calculate these values daily to assess any changes that may affect their positions or outlook, or simply to check if their portfolio needs to be rebalanced.
2. Can you name the five primary Greek in Options?
The most common Greeks used are
- Delta (Δ)
- Gamma (Γ)
- Theta (Θ)
- Vega (ν)
- Rho (Ρ)
3. Can you define Delta?
Delta (Δ): Delta measures the sensitivity of an option’s price to changes in the price of the underlying asset. It represents the rate of change in the option’s price with respect to a one-unit change in the underlying asset’s price. A delta of 0.50, for example, indicates that for every $1 increase in the underlying asset’s price, the option’s price is expected to increase by $0.50 if all other factors remain constant.
4. Can you define Gamma?
Gamma (Γ): Gamma measures the rate of change of an option’s delta with respect to changes in the price of the underlying asset. It provides insight into how delta itself changes as the underlying asset’s price changes. Gamma is particularly important for traders managing complex option positions and strategies.
5. Can you define Theta?
Theta (Θ): Theta measures the rate of decay in an option’s price as time passes. It quantifies the erosion of an option’s value due to the passage of time, assuming all other factors remain constant. Theta is often referred to as “time decay.” A higher theta means the option loses value more quickly over time.
6. Can you define Vega?
Vega (ν): Vega measures the sensitivity of an option’s price to changes in implied volatility. Implied volatility reflects the market’s expectations regarding future price fluctuations of the underlying asset. A higher vega indicates that the option’s price is more sensitive to changes in volatility. Traders use vega to assess how changes in volatility can impact option prices.
7. Can you define Rho?
Rho (ρ): Rho measures the sensitivity of an option’s price to changes in interest rates. It quantifies how much an option’s value changes with a one-percentage-point change in the risk-free interest rate. Rho is particularly relevant for options with longer maturities, as their values can be significantly affected by interest rate changes.
8. What is the range of Delta for a Call and Put option?
Delta for Call Options: The delta of a call option ranges from 0 to 1.
· A delta of 0 indicates that the call option has no sensitivity to changes in the price of the underlying asset. This would typically happen when the call option is significantly out-of-the-money (i.e., the strike price is much higher than the current price of the underlying asset).
· A delta of 1 indicates that the call option behaves almost identically to the underlying asset. As the price of the underlying asset increases by $1, the call option’s price also increases by approximately $1. This occurs when the call option is deep in-the-money (i.e., the strike price is much lower than the current price of the underlying asset).
Delta for Put Options: The delta of a put option ranges from -1 to 0.
· A delta of 0 indicates that the put option has no sensitivity to changes in the price of the underlying asset. This would typically happen when the put option is significantly out-of-the-money (i.e., the strike price is much lower than the current price of the underlying asset).
· A delta of -1 indicates that the put option behaves almost inversely to the underlying asset. As the price of the underlying asset increases by $1, the put option’s price decreases by approximately $1. This occurs when the put option is deep in-the-money (i.e., the strike price is much higher than the current price of the underlying asset).
9. What is the range of delta of call and put option with respect to its moneyness?
The range of delta for call and put options with respect to their moneyness is as follows:
For Call Options:
- Out-of-the-Money (OTM): The delta of an OTM call option typically ranges from 0 to 0.49.
- At-the-Money (ATM): The delta of an ATM call option is usually around 0.50.
- In-the-Money (ITM): The delta of an ITM call option typically ranges from 0.51 to 1.
For Put Options:
- Out-of-the-Money (OTM): The delta of an OTM put option typically ranges from -0.01 to -0.50.
- At-the-Money (ATM): The delta of an ATM put option is usually around -0.50.
- In-the-Money (ITM): The delta of an ITM put option typically ranges from -0.51 to -1.
10. What is the value of Delta for Long Call, Long Put, Short Call and Short Put position?
The delta for long call, long put, short call and short put are:
· Long Call Option: 0 to 1
· Short Call Option: 0 to -1
· Long Put Option: 0 to -1
· Short Put Option: 0 to 1
11. What is the formula of Delta for call and put option?
The formula for calculating the delta of a call option and a put option is as follows:
1. Delta for Call Option (Δc):
Δc = N(d1)
Where:
· Δc = Delta for the call option.
· N() = The cumulative standard normal distribution function.
· d1 = The formula for d1 is given by: d1 = (ln(S/K) + (r + (σ^2)/2) * T) / (σ * √T)
Where:
· S = Current price of the underlying asset.
· K = Strike price of the option.
· r = Risk-free interest rate.
· σ = Volatility of the underlying asset’s returns.
· T = Time to expiration of the option in years.
2. Delta for Put Option (Δp):
Δp = N(d1) – 1
Where:
· Δp = Delta for the put option.
· N() = The cumulative standard normal distribution function.
· d1 is the same as defined for the call option above.
These formulas provide the delta value for call and put options. Delta measures the sensitivity of the option’s price to changes in the price of the underlying asset. A positive delta for a call option indicates that its price increases as the underlying asset’s price rises, while a negative delta for a put option indicates that its price increases as the underlying asset’s price falls.
12. Can you draw the graph of delta of call and put option?
13. Example: Suppose stock XYZ was trading at $520 per share and a call option with a strike price of $500 was trading for $45. This call option is in-the-money because the stock price is above the strike price. If the price of XYZ stock rises to $523, and the value of the call option rises to $46.80. Find the delta of this option?
To solve the value of Delta, let us check the option price before and after the stock rose:
- Old Option Price = $45
- New Option Price = $46.80
- Old Stock Price = $520
- New Stock Price = $523
Delta = Change in Option Price / Change in Stock Price
Delta = (46.8 – 45) / (523 – 520)
Delta = 0.6
So, the delta of this call option is 0.60. This means that for every $1 increase in the price of the underlying stock (XYZ), the call option’s price is expected to increase by approximately $0.60, assuming all other factors remain constant. Since the call option is in-the-money, it has a delta greater than 0.5, indicating it is sensitive to changes in the stock price.
14. When the stock is trading at $125, the call option on the $140 strike with 80 days to expiry is worth $7.90. If the delta of the option is 0.39, what would be the price of the option when the stock is trading at $127?
Given:
- Delta of Call Option = 0.39
- Old Stock Price = $125
- New Stock Price = $127
- Old Option Price = $7.90
- New Option Price = Let us saw “X”
Delta = Change in Option Price / Change in Stock Price
0.39 = (X – $7.9) / ($127 – $125)
X – $7.9 = 0.39 * $2
X = $7.9 + $0.78
X = $8.68
Thus, the option will be worth $8.68.
15. What are the implications of Put Call Parity on Delta?
Put-Call Parity is a fundamental concept in options pricing that relates the prices of European call and put options with the same strike price and expiration date to the price of the underlying asset. It has important implications for understanding the relationships between the delta of call and put options and how they can change as market conditions or option parameters change.
Here are the key implications of Put-Call Parity on delta:
Put-Call Parity implies that the delta of a European call option minus the delta of the corresponding European put option is equal to 1. In other words:
Δc – Δp = 1
This relationship holds as long as the options are European-style, have the same strike price, and the same expiration date.
Where:
- Δc is the delta of the call option.
- Δp is the delta of the put option.
16. What are the limitations of Delta formula?
While the delta formula is a useful tool for estimating how an option’s price will change in response to changes in the price of the underlying asset, it has the following limitations that traders and investors should be aware of:
Constant Factors Assumption: The delta formula assumes that certain factors, such as volatility and interest rates, remain constant over the life of the option. In reality, these factors can change, and fluctuations in these variables can impact an option’s delta. Therefore, delta is a point-in-time estimate and may not accurately reflect future changes.
17. Explain the concept of Delta hedging and its importance in options trading.
Delta hedging is a risk management strategy used in options trading to reduce or eliminate the directional risk (i.e., exposure to price movements in the underlying asset) associated with holding options positions. It involves taking offsetting positions in the underlying asset to create a delta-neutral portfolio. In other words, delta hedging aims to make changes in the option’s value offset changes in the value of the underlying asset, resulting in a stable portfolio that is less sensitive to price movements.
Here’s how delta hedging works:
- Initial Position: Suppose you have a long call option, which means you have the right to buy the underlying asset at a specified strike price. Your initial position has a positive delta because the option’s value is positively correlated with the underlying asset’s price.
- Delta Measurement: Calculate the delta of your call option. This delta value represents how much your option’s price is expected to change for a $1 change in the underlying asset’s price.
- Offsetting Position: To create a delta-neutral portfolio, take a short position in the underlying asset. The size of the short position should be such that the delta of your options position and the delta of your short position cancel each other out. If your call option has a delta of 0.60, you would short 60 shares (0.60 * 100) of the underlying asset for each call option you hold.
- Portfolio Adjustment: As the underlying asset’s price changes, you will need to adjust your short position to maintain delta neutrality. When the underlying asset’s price rises, the delta of your call option increases, so you need to increase your short position to offset the rising delta. Conversely, when the underlying asset’s price falls, you decrease your short position.
18. What does Gamma measure in the context of Greek options?
Gamma represents the second derivative of an option’s price with respect to the price of the underlying asset. Mathematically, it can be expressed as the rate of change of delta (Δ) with respect to changes in the underlying asset’s price.
Gamma (Γ) = dΔ / Ds
Where:
- Γ is the gamma of the option.
- Δ is the delta of the option.
- dS represents small changes in the price of the underlying asset.
Gamma provides insight into how an option’s delta itself changes as the underlying asset’s price changes. It tells you how much the option’s delta will increase or decrease for a one-unit change in the underlying asset’s price.
19. How does Gamma change for a call option as the underlying asset’s price moves?
Gamma behaves differently for call and put options as the underlying asset’s price moves. Higher Gamma values indicate that the Delta could change dramatically with even very small price changes in the underlying stock or fund.
For Call Options:
Near At-the-Money (ATM): Gamma is highest for ATM call options. This means that the delta of an ATM call option is very sensitive to small changes in the price of the underlying asset. As the underlying asset’s price rises or falls, the delta of an ATM call option can change rapidly.
In-the-Money (ITM): Gamma for ITM call options is lower than for ATM options but still significant. As ITM call options move deeper ITM, gamma tends to decrease. However, it remains higher than that of out-of-the-money (OTM) call options.
Out-of-the-Money (OTM): Gamma is lowest for OTM call options. These options have less sensitivity to changes in the underlying asset’s price compared to ATM and ITM options. As a result, the delta of OTM call options changes relatively slowly in response to price movements in the underlying asset.
20. How does Gamma change for a put option as the underlying asset’s
price moves?
For Put Options:
Near At-the-Money (ATM): Similar to call options, gamma is highest for ATM put options. The delta of an ATM put option is very sensitive to small changes in the price of the underlying asset. As the underlying asset’s price rises or falls, the delta of an ATM put option can change rapidly.
In-the-Money (ITM): Gamma for ITM put options is lower than for ATM options but still significant. As ITM put options move deeper ITM, gamma tends to decrease. However, it remains higher than that of OTM put options.
Out-of-the-Money (OTM): Gamma is lowest for OTM put options. These options have less sensitivity to changes in the underlying asset’s price compared to ATM and ITM options. As a result, the delta of OTM put options changes relatively slowly in response to price movements in the underlying asset.
21. Can you draw the graph of gamma for an option?
The best way to understand the graph of gamma, is to take the graph of delta and differentiate it point-wise. We take the delta graph (red), find the tangent at each point (blue line), whose slope gives us the value of gamma (blue circle), which we then connect up to get the gamma curve (yellow).
22. What are the implications of put call parity on Gamma?
Put-call parity is a fundamental concept in options pricing that establishes a relationship between the prices of European call and put options with the same strike price and expiration date.
After differentiating the put call parity formula with respect to underlying, we can get the following formula:
Let’s differentiate this with respect to the underlying, and we obtain:
γc – γp = 0
γc = γp
As such, when we talk about the gamma of an option, we often do not need to specify whether it’s the put or the call. We can consider either scenario, and it often easier to consider call options which have a positive delta.
23. Apple stock is trading around $16.40. The call option on the $16 strike has a gamma of 0.617. What is the gamma of the put on the $16 strike?
We can use the put call parity formula to solve this question.
We know that the gamma of Call Option will be equal to gamma of Put Option
Therefore, Gamma of Put Option = 0.617
Note: Keep in mind that the underlying, strike and expiry should be same for call and put option.
24. What is Gamma Hedging?
Gamma hedging is a risk management strategy used by options traders and market makers to mitigate the exposure to changes in the delta of their options positions due to movements in the underlying asset’s price. It involves making adjustments to an options portfolio to keep it delta-neutral or to maintain a specific delta target.
Gamma Hedging Steps:
- Monitor Portfolio: Continuously monitor the deltas of the options in your portfolio.
- Adjust Delta: When gamma causes the delta of your portfolio to shift away from neutral, take action to bring it back to neutrality.
- Buy or Sell Options: To gamma hedge, you can buy or sell additional options to offset the changes in delta. If your delta becomes too positive (i.e., you become too long the underlying asset), you may sell options to reduce your delta. If it becomes too negative (i.e., you become too short the underlying asset), you may buy options to increase your delta.
25. What is Delta Gamma Hedging?
Delta gamma hedging, also known as gamma delta hedging, is an advanced options trading strategy used to simultaneously manage both delta and gamma exposure in an options portfolio. This strategy aims to maintain a balanced position that is not only delta-neutral (meaning the net directional exposure to the underlying asset is minimized) but also gamma-neutral (meaning the portfolio’s sensitivity to changes in delta is reduced).
A delta-gamma hedge is often one that is market-neutral (i.e., zero delta and zero gamma); however, a delta-gamma hedge can, in theory, adopt any static level of delta and/or gamma. Options positions that are delta-gamma hedged are still exposed to changes in value, due to shifts in volatility, interest rates, and time decay.
26. What is Theta, and why is it also known as “time decay”?
Theta, often referred to as “time decay,” is one of the Greek letters used in options trading to measure the rate at which the value of an option erodes as time passes. Theta reflects how sensitive an option’s price is to the passage of time. As each day passes, the value of the option decreases, all else being equal. This is because, with each passing day, there is less time for the option to move in a favorable direction for the holder.
Theta is not linear but follows an exponential decay curve. This means that the closer an option is to its expiration date, the faster its time decay accelerates. In the final weeks or days before expiration, theta can erode the option’s value rapidly. Theta is generally expressed as a negative number for long positions and as a positive number for short positions. It can be thought of as the amount by which an option’s value declines every day.
27. How does theta behave when option reaches maturity?
As expiration gets closer, the time value of an options contract decreases. Before expiration, the time value of an option is at least 0. The longer the time until an options contract expires, the greater the opportunity for the underlying security’s price to move and increase its intrinsic value, so the contract has more time value. Basically, with more time on the clock, more price movement can happen.
Time decay, theta burn, and theta decay are synonymous and refer to the decline in the value of an options contract as expiration approaches. Time decay is non-linear, meaning the rate of change increases as the options contract approaches expiration.
The time value of an options contract decreases at an accelerating rate as expiration approaches. For example, time decay increases more rapidly from 60 to 30 days than from 90 to 60 days. While an option’s time value decreases over time, other extrinsic factors, like implied volatility, may increase as expiration approaches, offsetting or exceeding theta decay. Still, it is important to know options are decaying assets and lose time value daily.
28. How do you calculate theta?
The formula for theta (θ) in options pricing can vary slightly depending on the pricing model being used, such as the Black-Scholes model or the Binomial model. However, the basic formula for theta is as follows:
θ = – dV/dt
Where:
- θ (Theta) is the symbol for the option’s theta.
- dV represents the change in the option’s value.
- dt represents the change in time.
Theta is quoted in dollars and represents the amount the option’s price will decrease each day. For example, a theta value of -0.02 means the option will lose $0.02 ($2) per day. Theta is always represented in negative terms because the portion of an option’s premium related to time is always going down.
Theta value is smaller further away from expiration and is not constant–it accelerates the closer it gets to expiration. Theta is an advantage for the option seller and a disadvantage for the option buyer.
Circling back to the moneyness discussion from the introduction, theta varies depending on a contract’s strike price relative to the underlying asset’s price. This options Greek is known as delta. While theta decay occurs across all strike prices, the fastest decay occurs for contracts at-the-money. Contracts further out-of-the-money decay more linearly.
29. Which Option Has the Highest Theta?
Options with the highest theta are typically at-the-money (ATM) options with short time to expiration. Let’s break down why this is the case:
At-the-Money (ATM) Options: ATM options are those where the strike price is very close to the current market price of the underlying asset. These options tend to have the highest theta because they have the most time value relative to their intrinsic value. Time value is what decays overtime, so options with more time value will experience greater theta decay. Therefore, the highest theta is for at-the-money options and the lowest theta is for the furthest out-the-money and in-the-money options.
Short Time to Expiration: Options with a shorter time to expiration have higher thetas compared to options with longer timeframes. This is because time decay accelerates as options approach their expiration date. Short-term options experience more rapid erosion of their time value, resulting in higher thetas.
30. What is the effect of theta for option buyer and seller?
Theta measures the rate at which an option’s price is expected to decay for each day that passes, assuming that all other factors remain the same. This rate of decay tends to accelerate as the option approaches its expiration date, a phenomenon often referred to as “time decay.”
Here’s how theta works for options buyers versus options sellers:
Options Buyers: If you’re the holder (buyer) of an option, theta can work against you. Each day that passes reduces the amount of time for the option to become profitable (or more profitable if it’s already in-the-money). For instance, if you own a call option with a theta of -$0.05, the extrinsic value of your call option will drop by $0.05 ($5) per day, all other things being equal.
Options Sellers: If you’re the writer (seller) of an option, theta can work in your favor. The premium you received when you sold the option gradually decays as time passes. That’s because with each passing day, there’s theoretically less time for the underlying asset to move in a way that would make the option profitable for the buyer. If the option is out-of-the-money at expiration, it will expire worthless, and as the seller, you get to keep the entire premium received up front on trade entry.
31. Imagine you buy a call option for $2.00 with a strike price of $50 that expires in 30 days. The underlying stock is currently trading at $48. Now, let’s say this option has a theta of -0.05. What inference can you make by this?
This means – all else being equal – the price of your option will decrease by $0.05 each day due to time decay. So, after one day, if all the other factors remain unchanged, your option might be worth $1.95 (down from the initial $2.00). And after two days, it would theoretically be worth $1.90.
However, theta decay can accelerate as the option gets closer to expiration, which is something to keep in mind.
32. Is theta good or bad?
Whether theta is “good” or “bad” in options trading depends on your position and your trading strategy.
If you’re an option buyer, theta is often considered a potential negative. That’s because theta represents the rate at which a long option’s extrinsic value decays over time—so, as time passes, long options lose value, all else being equal.
On the other hand, if you’re an option seller, theta is often considered a positive. That’s because as time passes, the short option position theoretically loses value, which may allow the investor/trader to buy it back for a lower value, or even expire worthless. But it’s important to note that a short options position isn’t guaranteed to turn a profit, just as a long options position isn’t guaranteed to turn a profit.
33. Define Vega?
Vega quantifies how much an option’s price will change for a one-percentage-point change in implied volatility, assuming all other factors remain constant.
Vega is one of the Greek letters used in options trading to measure an option’s sensitivity to changes in implied volatility. Implied volatility represents the market’s expectation of how much an underlying asset’s price will fluctuate in the future. Higher implied volatility generally leads to higher option premiums, and lower implied volatility leads to lower option premiums. Therefore, options with higher Vega values are more sensitive to changes in implied volatility.
34. What is positive vs negative Vega?
Positive Vega: Most long options (options that are bought) have positive Vega. This means that when implied volatility rises, the value of these options increases, and when implied volatility falls, their value decreases.
Negative Vega: Most short options (options that are sold) have negative Vega. This means that when implied volatility rises, the value of these options decreases, and when implied volatility falls, their value increases. Option sellers benefit from a decrease in implied volatility.
35. What effect Vega has on long call, long put, short call and short put?
Vega has different effects on long call, long put, short call, and short put options, depending on whether the options are bought (long) or sold (short). Here’s how Vega influences each of these option positions:
a) Long Call Option: Long call options have positive Vega. This means that when implied volatility increases, the value of a long call option rises, and when implied volatility decreases, the value falls. Positive Vega benefits long call holders because they profit from rising volatility, which increases the chances of the underlying asset making larger price moves, potentially resulting in higher option prices.
b) Long Put Option: Long put options also have positive Vega. Like long calls, when implied volatility increases, the value of a long put option rises, and when implied volatility decreases, the value falls. Positive Vega benefits long put holders because they profit from rising volatility, which can lead to larger price swings and higher put option values.
c) Short Call Option (Call Writer): Short call options have negative Vega. This means that when implied volatility increases, the value of a short call option decreases, and when implied volatility decreases, the value rises. Negative Vega benefits short call writers because they profit from falling or stable volatility. Reduced volatility often leads to smaller price swings, which can result in a decline in the value of short call options.
d) Short Put Option (Put Writer): Short put options also have negative Vega. Like short calls, when implied volatility increases, the value of a short put option decreases, and when implied volatility decreases, the value rises. Negative Vega benefits short put writers because they profit from falling or stable volatility. Reduced volatility typically results in smaller price swings, which can lead to a decrease in the value of short put options.
In summary, Vega affects option positions as follows:
Long call and long put options have positive Vega, so they benefit from rising implied volatility. Short call and short put options have negative Vega, so they benefit from falling or stable implied volatility.
36. How maturity affects Vega?
Maturity, or the time to expiration, can have a significant effect on Vega, the sensitivity of an option’s price to changes in implied volatility. The relationship between maturity and Vega is as follows:
Longer Maturity Options Have Higher Vega: Options with longer time to expiration tend to have higher Vega values. This means that their prices are more sensitive to changes in implied volatility compared to options with shorter maturities.
For example, if you compare two otherwise identical call options, one with an expiration of one year and the other with an expiration of one month, the one-year option is likely to have a higher Vega because it has more time for implied volatility to potentially change.
Shorter Maturity Options Have Lower Vega: Conversely, options with shorter time to expiration tend to have lower Vega values. This means that their prices are less sensitive to changes in implied volatility compared to options with longer maturities. Continuing with the example, the one-month option is likely to have a lower Vega compared to the one-year option because there is less time for implied volatility to have a significant impact.
37. When is Vega highest?
Vega is typically highest for at-the-money (ATM) options that have longer times to expiration.
Longer Time to Expiration: Options with longer times to expiration generally have higher Vega values. This is because options with more time until expiration have more time value, and therefore, changes in implied volatility have a larger impact on their prices. ATM options with longer expirations, are more sensitive to changes in implied volatility because there is more time for potential price movements in the underlying asset to occur.
Vega Tends to Peak at ATM: Vega is not constant across all strike prices and maturities. It often peaks for ATM options with longer maturities because these options have the most time value and are highly sensitive to changes in implied volatility.
38. How does market news affect implied volatility?
Events such as earnings announcements, economic data releases, geopolitical developments, or market shocks can lead to changes in implied volatility. Traders use Vega to assess how these events might affect their options positions. Options with higher Vega are more sensitive to changes in implied volatility and may experience larger price swings during such events.
39. When the stock is trading at $45, the call option on the $45 strike with 25 days to expiry is worth $3.48 at an implied volatility of 62. If the vega of the option is 0.056, what would be the price of the option when implied volatility is 70?
Answer
- Call Option Price = $3.48
- Implied Volatility = 62
- Vega = 0.056
- Price of the option when implied volatility is 70?
Vega = (Change in Option Price)/(Change in Implied Volatility)
0.056 = (X – 3.48) / (70 – 62)
X – 3.48 = 8 * 0.056
X = 3.48 + 0.448
X = $3.928
40. What are the implications of Put-Call Parity on Vega?
This tells us that the vega of the call and the put on the same strike and expiration is the same. Thus, to know the vega of an option on a strike, we can consider either the call or the put option.
41. How do you calculate implied volatility?
There are several mathematical models and methods used to calculate implied volatility in options pricing. Implied volatility is the market’s expectation of future price volatility implied by the current option prices. Here are some common models and methods to calculate implied volatility:
Black-Scholes Model: The Black-Scholes model is one of the most well-known and widely used models for calculating implied volatility. It is used primarily for European-style options and assumes constant volatility. To calculate implied volatility using this model, traders typically use option pricing formulas and solve for the volatility parameter, which results in implied volatility.
Binomial Model: The Binomial model, such as the Cox-Ross-Rubinstein (CRR) model, is another approach to estimate implied volatility. It is often used for American-style options and allows for multiple time steps. Implied volatility can be calculated iteratively by adjusting the volatility parameter until the model’s option price matches the market price.
GARCH Models: Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models are commonly used for modeling and forecasting financial time series, including implied volatility. GARCH models capture the volatility clustering and time-varying characteristics often observed in financial data. You can apply GARCH models to the residuals of option pricing models to capture implied volatility dynamics.
Stochastic Volatility Models: Stochastic Volatility (SV) models, like the Heston model, assume that volatility itself follows a stochastic process. These models allow for time-varying volatility and can be used to analyze and forecast implied volatility time series. The Heston model, in particular, is popular for this purpose.
Machine Learning Models: Machine learning techniques, such as neural networks, random forests, and support vector machines, can be used for forecasting implied volatility time series. These models can capture complex patterns in the data and may outperform traditional statistical models in certain situations.
42. What is Rho in Greek Options?
Rho measures the expected change in an option’s price per one-percentage-point change in interest rates. It tells you how much the price of an option should rise or fall if the risk-free interest rate (U.S. Treasury-bills) increases or decreases.
43. What is positive and negative Rho?
Interest rate increases usually increase the value of long options calls and decrease the value of short options puts. Therefore, long calls and short puts have a positive rho; long puts and short calls have a negative rho.
However, the truth is that rho is not a factor that ordinarily has a significant effect on option prices. Interest rates tend to only significantly shift option prices when there is a major and/or unexpected change in the risk-free rate. For example, if an announcement were made following a Federal Open Market Committee (FOMC) meeting that the Fed was decreasing the prime lending rate by half a percent – and the decrease in rates was very unexpected – then rho would likely have a significant impact on option prices. However, it would really just be in line with the overall market impact of such a sudden, unexpected rate change, which would most likely lead to notably increased market volatility, which, in turn, is typically reflected in higher option prices.
44. Why is Rho positive for long call options?
A call option’s value typically increases when interest rates rise. Buying call options may be a better use of capital than purchasing stock in a high interest rate environment because a long call option requires less capital than buying shares of stock. The money saved can then be allocated to high yielding investments such as bonds.
Since call options give the holder the right to buy the underlying asset at a specified strike price, they benefit from lower financing costs associated with higher interest rates. When interest rates rise, the opportunity cost of holding cash increases, making call options relatively more attractive. This results in an increase in the value of call options.
45. Why Rho is positive for short put option?
Short put options involve selling (writing) a put contract, which obligates the seller to potentially buy the underlying asset at a specified strike price if the option is exercised by the buyer. When interest rates rise, the opportunity cost of holding cash increases, making it more attractive to sell (write) put options. This results in an increase in the premium received for selling the put option.
46. What implications do rising interest rates have for traders and investors in the options marketplaces?
The most common way to trade options is via standardized contracts on exchanges. The prices of these contracts are generally a function of the underlying asset, which in most cases is a stock or index.
When interest rates rise, it affects the required rate of return that investors demand from holding stocks. This, in turn, will affect the prices of options contracts. Higher rates make it more expensive to hold certain investments as the opportunity cost of holding the underlying asset increases.
Investors must consider the opportunity cost of options compared to buying or selling stocks as interest rates rise. For example, a long call option requires less capital than buying shares of stock. So, if you purchase a call option contract when interest rates are relatively high, the money you save not purchasing shares could be allocated to high yielding, fixed-income securities.
47. What Is Vanna in Options?
Vanna is a second-order derivative that measures the change in delta for any change in the implied volatility of an option. It is measured as the change in delta for every 1% change in implied volatility. In options trading, vanna will be negative for put options and positive for call options. Positive Vanna means the delta becomes more positive (moves toward +1) when IV increases, while negative Vanna means the delta becomes more negative (moves toward -1) when IV increases.
Overall, Vanna is one of the many risk metrics and tools that options traders use to understand and manage the complexities of options trading. It’s especially important for traders who want to be precise in their risk assessment and portfolio management.
How does delta change when implied volatility changes? This measurement is called “vanna.” Because vanna is a derivative of delta, it is categorized as a “second-order” Greek.
48. Why Vanna is important?
Hedging: Options traders often use Vanna as part of their risk management and hedging strategies. By understanding how their delta changes with respect to changes in volatility, they can make more informed decisions about when to adjust or hedge their positions.
Volatility Trading: Some traders specialize in trading volatility itself, often referred to as “volatility trading” or “volatility arbitrage.” Vanna is a crucial metric for such traders as it helps them exploit changes in implied volatility to profit.
Managing Risk: Vanna helps traders assess and manage their risk exposure. It provides insight into how changes in implied volatility can affect the overall risk of an options portfolio.
49. What is Charm (Delta decay)?
Charm, or delta decay, is the rate at which the delta of an option or warrant changes with respect to time. Charm values range from -1.0 to +1.0, with in-the-money options tending toward 100 delta and out-of-the-money options toward zero as expiration approaches.
For example, if charm of a call option is 0.05, it means the delta of the option will increase by 0.05, if there is one-day decrease in time to expiration.
Charm can be used to manage the risk exposure of an options position by measuring how changes in time to expiration affect the position’s delta. By understanding the impact of changes in time to expiration on delta, traders can adjust their positions to better manage risk.
50. Can you describe Zomma in Greeks?
Zomma is one of the lesser-known Greek risk measures in options trading, and it measures the sensitivity of an option’s gamma (Γ) to changes in the underlying asset’s price. Gamma, as a reminder, measures how fast the option’s delta (Δ) changes with changes in the underlying asset’s price. Specifically, Zomma quantifies how much the option’s gamma will change for a one-point (or one-unit) change in the price of the underlying asset.
Interpretation: A positive Zomma value indicates that the gamma is expected to increase as the underlying asset’s price changes, while a negative Zomma value means the gamma will decrease as the underlying asset’s price changes.
Options traders often use Zomma to assess the risk profiles of their options portfolios, particularly when they have positions with significant gamma exposure. Understanding Zomma can help traders determine how their portfolio’s delta will change in response to price movements and make informed hedging or adjustment decisions.